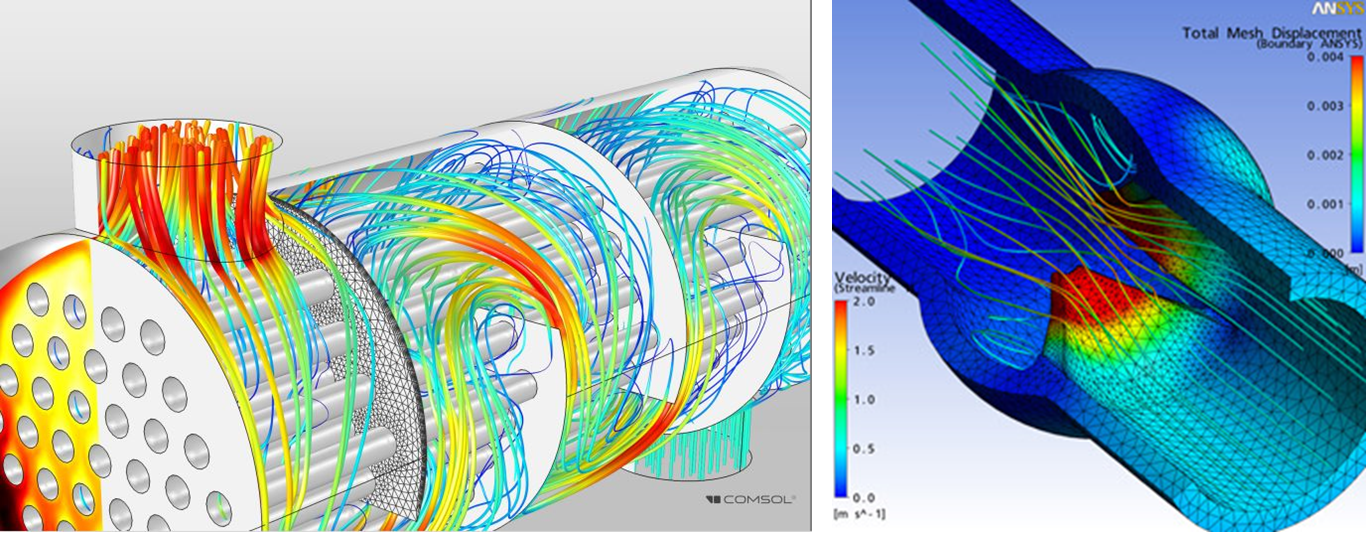
Цифрове моделювання

дослідження об'єктів (явищ, процесів, пристроїв, систем тощо) за допомогою математичних моделей на ЕОМ. Комп'ютерні моделі стали звичайним інструментом математичного моделювання і застосовуються у фізиці, астрофізиці, механіці, хімії, біології, економіці, соціології, метеорології, інших науках і прикладних задачах в різних областях радіоелектроніки, машинобудування, автомобілебудування та ін. Комп'ютерні моделі використовують для отримання нових знань про об'єкт чи для наближеної оцінки поведінки систем, занадто складних для аналітичного дослідження.

Задачі математичних моделей

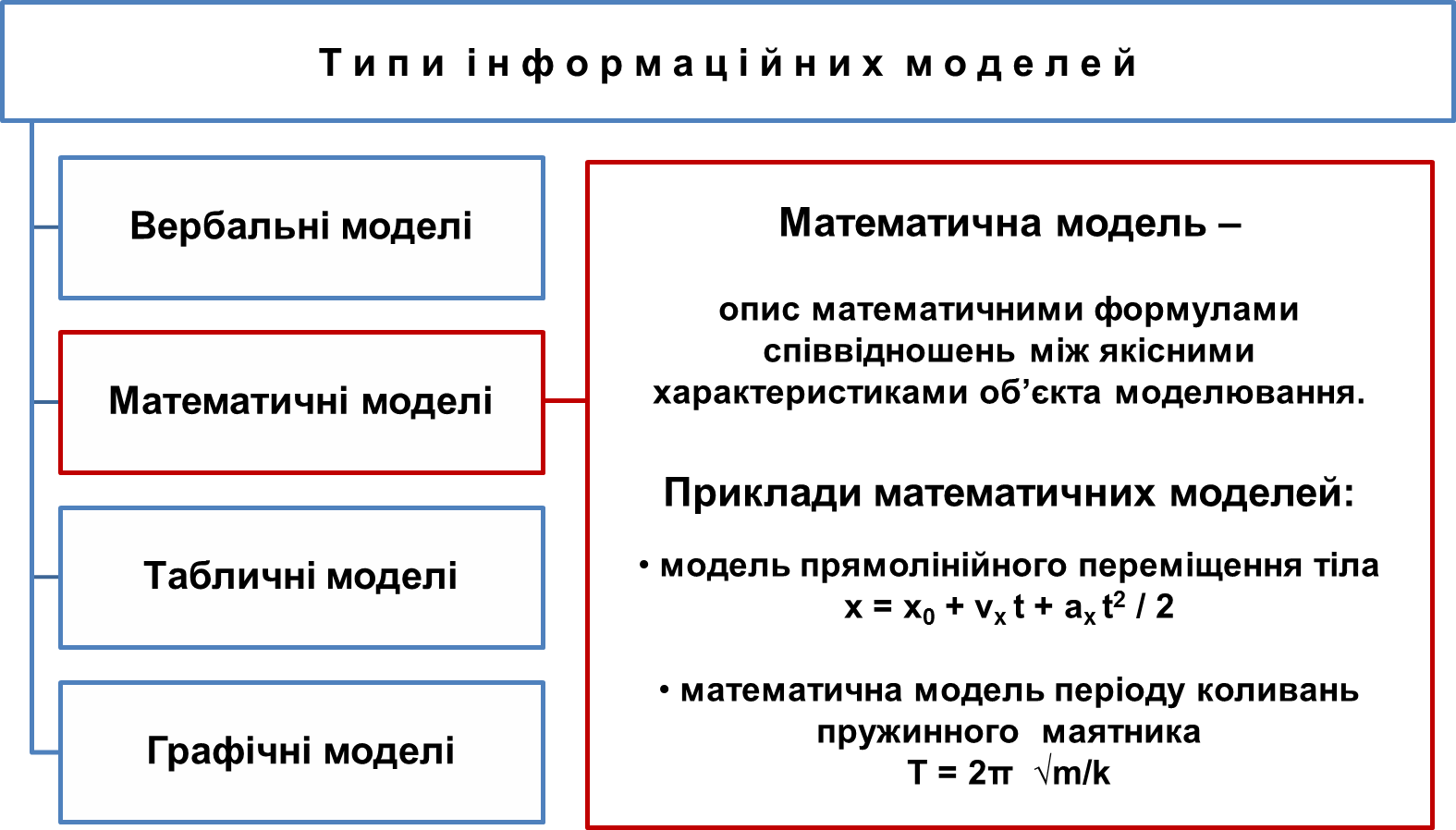Для кожної математичної моделі формулюється відповідна математична задача. При цьому відповідно до виду математичної моделі розрізняють такі базові типи математичних задач:

• розв’язання систем лінійних (лінеаризованих) рівнянь;
• розв’язання нелінійних алгебраїчних рівнянь;
• апроксимація масиву даних або складної функції набором стандартних, більш простих функцій;
• розв’язання диференціальних рівнянь;
• розв’язання інтегральних рівнянь;
• інші задачі.

Для розв’язання цих та інших задач застосовують чисельні методи – математичний інструментарій, за допомогою якого математична задача формулюється у вигляді, зручному для розв’язання на ЕОМ.

Вимоги до математичних моделей

Математична модель є математичним аналогом проектованого об'єкта. Ступінь її адекватності об'єкту визначається постановкою і коректністю рішень задачі проектування. Основними вимогами, що пред'являються до математичних моделей, є вимоги адекватності, універсальності і економічності.
Адекватність. Модель вважається адекватною, якщо відображає задані властивості з прийнятною точністю. Точність визначається як ступінь збігу значень вихідних параметрів моделі та об'єкта.
Універсальність - визначається в основному числом і складом врахованих в моделі зовнішніх і вихідних параметрів.
Економічність моделі характеризується витратами обчислювальних ресурсів для її реалізації - витратами машинного часу і пам'яті.

Вивчення курсу “Математичне моделювання”

Мета вивчення дисципліни – вивчення базових  понять, основних принципів і методів математичного моделювання.

Завдання дисципліни:

• Формування уявлень про види інформаційних моделей та математичну модель зокрема, а також способи представлення математичних моделей та вимоги до них; методи отримання математичних моделей та можливості їх застосування; програмні засоби математичного моделювання;
• Формування знань числових методів розв’язання рівнянь та їх систем як засобів математичного моделювання, а також умінь і навичок застосування цих методів на практиці.

Під час вивчення дисципліни студенти прослуховують лекції на наступні теми: “Основні поняття математичного моделювання”, “Розв’язання лінійних і нелінійних рівнянь”, “Пошук екстремуму функції”, “Розв’язання систем лінійних алгебраїчних рівнянь” тощо. А також виконують комп’ютерні практикуми на відповідні теми.